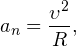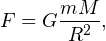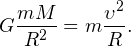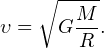Чем ближе спутник к земле тем скорость
Cкорость движения спутника вокруг Земли
В космосе гравитация обеспечивает силу, из-за которой спутники (такие, как Луна) вращаются по орбитам вокруг более крупных тел (таких, как Земля). Эти орбиты в общем случае имеют форму эллипса, на чаще всего, этот эллипс не сильно отличается от окружности. Поэтому в первом приближении можно считать орбиты спутников круговыми. Зная массу планеты и высоту орбиты спутника над Землей, можно рассчитать, какой должна быть скорость движения спутника вокруг Земли.
Расчет скорости движения спутника вокруг Земли
Вращаясь по круговой орбите вокруг Земли, спутник в любой точке своей траектории может двигаться только с постоянной по модулю скоростью, хотя направление этой скорости будет постоянно изменяться. Какова же величина этой скорости? Её можно рассчитать с помощью второго закона Ньютона и закона тяготения.
Для поддержания круговой орбиты спутника массы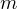 
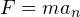
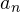
в соответствии со вторым законом Ньютона потребуется центростремительная сила: 
, где 
— центростремительное ускорение.
Как известно, центростремительное ускорение определяется по формуле:
где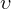 
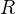
— скорость движения спутника, 
— радиус круговой орбиты, по которой движется спутник.
Центростремительную силу обеспечивает гравитация, поэтому в соответствии с законом тяготения:
Подставляя все в исходную формулу, получаем:
Выражая искомую скорость 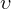, получаем, что скорость движения спутника вокруг Земли равна:
Это формула скорости, которую должен иметь спутник Земли на заданном радиусе 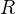(т.е. расстоянии от центра планеты) для поддержания круговой орбиты. Скорость не может меняться по модулю, пока спутник сохраняет постоянный орбитальный радиус, то есть пока он продолжает обращаться вокруг планеты по круговой траектории.
При использовании полученной формулы следует учитывать несколько деталей:
Искусственные спутники Земли, как правило, обращаются вокруг планеты на высоте от 500 до 2000 км от поверхности планеты. Рассчитаем, с какой скоростью должен двигаться такой спутник на высоте 1000 км над поверхностью Земли. В этом случае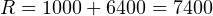 
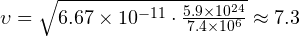
км. Подставляя числа, получаем:
км/с.
Материал подготовлен репетитором по математике и физике в Москве, Сергеем Валерьевичем
Причины особенностей движения спутников
Кузнецов А.И., Кузнецов А.Р.
Не смотря на многовековую историю изучения движения небесных тел, до настоящего времени отсутствуют конкретные представления о физической сущности и факторах, определяющих место расположение и характер вращения спутников как по орбитам, так и вокруг собственной оси. В основе современной теории их движения лежат сложные математические модели, получаемые методом подгонки под существующие результаты наблюдений за их положением в процессе их движения в конкретные периоды времени. Такие модели могут описать движение спутников для сравнительно небольшого участка их орбиты и действуют только в течение определенного промежутка времени.
В прошлые века теории опирались исключительно на модели кеплеровского движения и законы ньютоновской механики. Однако, из-за большой погрешности между фактическим положением тел и получаемыми расчетными данными в дальнейшем к модели начали добавляться возмущения от различных факторов. Это привело к тому, что, с увеличением требований к точности, исследователи выводили чрезвычайно объемные уравнения. Современные аналитические теории движения планет и спутников весьма громоздки и сложны. Кроме того, их постоянно приходится корректировать с учетом вновь полученных результатов наблюдений за их фактическим положением. Постепенно, этот снежный ком данных настолько вырос, что даже самые быстродействующие вычислительные машины не в состоянии справиться с таким объемом информации.
За исключением нескольких простейших механических моделей, точного аналитического решения общей задачи получить невозможно. К тому же, никакое аналитическое решение не будет справедливо на бесконечном интервале времени [1].
К примеру, с древних времён люди пытались описать и объяснить движение Луны, но безуспешно. Основой современных расчётов является теория Брауна, в которой используется более 1400 членов (коэффициентов и аргументов при тригонометрических функциях).
Реальное движение Луны довольно сложное, при его расчёте принято учитывать множество факторов, например, сплюснутость Земли и сильное влияние Солнца, которое притягивает Луну в 2,2 раза сильнее, чем Земля. Более точно движение Луны вокруг Земли можно представить, как сочетание нескольких более простых движений. Исходными данными являются результаты измерений дальности расположения Луны с помощью лазерной локации, установленных на ней, уголковых отражателей [1].
Вводя новые факторы, почему-то, никто не задумывается и не пытается их объяснить. Например, если в основе движения небесных тел лежит закон всемирного тяготения (гравитация) и Солнце притягивает Луну в 2,2 раза сильнее, чем Земля, то почему она до сих пор вращается вокруг Земли, а не Солнца.
Большинство наблюдаемых, наиболее крупных и близких спутников Солнечной системы обращается вокруг своих планет в том же направлении, в котором происходит осевое вращение планет. Орбиты таких спутников обычно круговые или близкие к ним и лежат вблизи плоскости экватора планеты.
Четкая, обоснованная природа наблюдаемых явлений до настоящего времени отсутствует. Как для других спутников, так и для Луны в частности, не понятны такие закономерности, как:
1. Расположение орбиты спутников именно в районе экватора, а не полюсов, например, или еще где.
2. Наклон орбиты Луны к плоскости Земной орбиты составляет примерно 5 градусов.
3. Наличие орбитального ускорения некоторых спутников.
4. Постепенное удаление Луны от Земли примерно на 4 см в год, в следствие чего её орбита представляет собой медленно раскручивающуюся спираль.
5. Постоянное расположение их, в процессе вращения, к планете одной и той же стороной.
Все перечисленные загадочные явления легко объясняются согласно предложенной нами гипотезы вращения планет Солнечной системы по орбите и вокруг собственной оси. Их положение на орбите и вращение определяется воздействием исходящего снизу от Солнца потока солнечного ветра, вращающегося по конической спирали против часовой стрелки, а сверху опускающегося вниз по внутренней стороне конуса газового потока, вращающегося по часовой стрелке [2].
Такое движение, при обтекании планет (с учетом их атмосферы) сверху и снизу, формирует в районе экватора газодинамическую структуру, включающую область взаимодействия двух соосных встречных сверхзвуковых потоков, в которой сталкивающиеся газы разрежены. Существенной особенностью такой структуры является формирование веерного расширения образующейся смеси газов в пространстве, окружающем плоскость симметрии области взаимодействия потоков [3].
Рассмотрим, с использованием предложенной нами гипотезы, природу перечисленных выше закономерностей поведения спутников в приведенном там порядке:
1. Образование зоны взаимодействия (завихрения) потоков и веерного расширения смеси газов в направлении от планеты, способствует созданию в районе экватора области пониженного давления, которая на Земле распространяется по высоте примерно на 10 градусов широты по обе стороны от экватора.
Именно под воздействием этих потоков орбита спутников, в т. ч. Луны, располагается в месте их стыковки, на линии экватора.
Расположение спутников, характер их движения и расстояние между планетой и спутником (диаметр орбиты) обусловлены влиянием зоны взаимодействия внешнего и внутреннего спиральных потоков, обтекающих планету (рис. 1). Высота и ширина распространения зоны взаимодействия (завихрения) зависит от скорости и плотности этих потоков.
2. При столкновении этих потоков в районе экватора, они образуют вращающуюся вокруг планеты зону взаимодействия (завихрения). Характер вращения зоны, а вместе с ней и спутников, определяется воздействием на них существующего направления движения потоков, планеты и ее атмосферы.
Результирующая сила Fв, возникающая от взаимодействия двух потоков и их веерного расширения, будет действовать по периметру планеты (от нее) в радиальном направлении от линии ее экватора. Давление внутри этой зоны, «вблизи» планеты, будет минимальным, постепенно увеличиваясь по мере ее удаления от поверхности. Возникающая вследствие этого центростремительная сила Fц, будет действовать в плоскости экватора по направлению к планете, удерживая спутник на орбите и заставляя его вращаться вместе с этой зоной вокруг планеты в направлении ее вращения [2].
Учитывая наибольшую силу воздействия внешнего потока, движущегося от Солнца вверх (рис.1, б), орбита спутника в данном месте будет приподнята кверху. Соответственно под давлением внутреннего потока, опускающегося вниз (рис. 1, а), его орбита будет наклонена книзу. Вследствие этого орбита Луны имеет наклон примерно 5 градусов.
3. Луна (спутник) двигаясь вместе с зоной взаимодействия по орбите вокруг планеты, при попадании в поле действия внутреннего потока (рис. 1, а), направление которого совпадает с направлением его движения, приобретает дополнительное орбитальное ускорение. Аналогичное воздействие оказывает внешний поток при попадании Луны (спутника) в поле его воздействия (рис. 1, б). Этим объясняется наличие орбитального ускорения спутников.
4. Положение орбиты спутника (удаленность) от планеты определяется уравновешиванием воздействия на него силы взаимодействия Fв (веерного расширения), направленной от планеты, с центростремительной силой Fц зоны разрежения, направленной в сторону планеты. Это равновесие поддерживается на всем участке орбиты спутника, за исключением зоны действия опускающегося внутреннего потока (рис. 1, а). При движении на этом участке на спутник действует дополнительная центростремительная сила Fцв разряжения в центре воронки внутреннего спирального потока. Под действием этой силы происходит постепенное удаление Луны (спутника) от Земли (планеты) примерно на 4 см в год, в следствие чего её орбита представляет собой медленно раскручивающуюся спираль.
5. В результате совпадения направлений вращения зоны взаимодействия (завихрения) и внутреннего, и внешнего потоков, в месте их соприкосновения (рис. 1), на спутник действует движущая его сила только в одном направлении, заставляя его обращаться вокруг планеты.
Из классической физики известно, что при отсутствии у тела жестких связей, его вращение вокруг собственной оси возможно только при одновременном воздействии на него двух противоположно направленных параллельных сил, расположенных по разные стороны от его оси. При этом характер вращение тела определяется направлением воздействия вращающего момента, создаваемого этими силами.
Действие только одной силы придает спутнику (например, Луне) направленное движение по орбите без вращения вокруг собственной оси (рис.1), т.е. постоянное расположение его, в процессе вращения, к планете одной и той же стороной.
В научных кругах последнее явление принято называть синхронным вращением или приливным захватом. Однако, при расположении наблюдателя, на планете, такое осевое их вращение совсем незаметно. Поэтому, на протяжении столетий длятся споры на тему, существует ли на самом деле вращение спутников, в частности Луны, вокруг своей оси или нет. Общеизвестный пример движения человека вокруг стола, в положении лицом к нему, ничего не доказывает. Это вращение его вокруг собственной оси чисто условное. С таким же успехом можно сказать, что, при вращении велосипедного колеса вокруг оси, штуцер, находящийся на ободе, также совершает вращение вокруг собственной оси, хотя всем ясно, что он закреплен неподвижно.
Постоянным воздействием (давлением) спиральных потоков в районе полюсов, очевидно, можно объяснить существующую сплюснутость (эллипсоидность) спутников и планет, особенно газовой группы, в направлении оси их вращения. Поскольку при столкновении потоков с поверхностью тела, происходит уменьшение их кинетической энергии, сопровождающееся выделением тепла, то это позволяет объяснить скопление на полюсах большинства планет Солнечной системы, в частности в Арктике и Антарктиде толстого слоя льда.
Наличие пониженного атмосферного давления и постоянство места взаимодействия потоков, сопровождающееся выделением тепла, обуславливает наличие на Земле в экваториальной зоне влажного климата со стабильной температурой. В течение года ее колебания составляют всего около 1 градуса.
Происхождение колец Сатурна до сих пор остается предметом дискуссий. По одной из версии, они возникли вместе с планетой. По другой — кольца образовались относительно недавно в результате разрушения одного из его спутников [4].
Согласно нашей гипотезы основными причинами этого являются:
— образование зоны взаимодействия спиральных потоков;
— повышенное содержание водорода в атмосфере газовых планет;
— наличие здесь относительно низких температур.
Известно, что при низких температурах водород переходит в твердую снегообразную фазу. Видно, она то и является основой появления льдинок в кольцах из облаков атмосферы этих планет. Это происходит аналогично образованию льдинок града в тучах в атмосфере Земли, но, вероятно, без участия кислорода.
Самые высокие облака в атмосфере Сатурна наблюдаются именно над экватором на уровне давления 0,07 атмосфер и высоте около 100 км над основным уровнем облаков [4].
Небольшое количестве спутников из скальных пород и полное отсутствие ледяных в зоне планет земной группы объясняется их более близким расположением к Солнцу, наличием сравнительно высоких температур и незначительным содержанием водорода в атмосфере.
Твердая фаза водорода так же является, очевидно, основной составляющей комет в космосе и белых «шапок» на полюсах планет Солнечной системы. Мы считаем, что она же лежит в основе образования гигантского шестиугольника, на северном полюсе Сатурна, не имеющего пока научного объяснения. Причиной его образования, вероятно, являются те же физические процессы, что и при образовании геометрически правильной шестиугольной формы снежинок и льдинок в условиях Земли.
Толщина колец Сатурна составляет всего несколько сотен метров, а ширина – десятки тысяч километров. Сразу после того как они были открыты, у астрономов возник первый вопрос: почему они плоские и тонкие? Считаем, что геометрические размены колец определяются размерами зоны взаимодействия спиральных потоков, которая в свою очередь, зависят от их скорости и плотности. По мере удаления от Солнца скорость спиральных потоков и их плотность уменьшаются, а, следовательно, будет уменьшаться толщина зоны взаимодействия и толщина колец.
Из закона о характере распределения тел внутри вращающегося потока известно, что более крупные и тяжелые тела будут располагаться во внешней части потока, а более мелкие и легкие – во внутренней.
Последнее свидетельствует о наличии внутри зоны взаимодействия завихрений, возникающих от столкновения и перемешивания спиральных потоков.
Скорости ветра на Сатурне достигают 400-500 м/сек. Ветры дуют параллельно экватору в прямом направлении. Скорости ветра значительно различаются на разных широтах. В зонах взаимодействия ветровых течений образуются штормовые системы и вихри аналогично Большому Красному Пятну на Юпитере [4].
Сатурн не единственная планета Солнечной системы, обладающая кольцами. Они обнаружены также у Юпитера, Урана и Нептуна. Их кольца, скорее всего, имеют ту же природу, но гораздо менее заметные.
По нашей гипотезе, спутники подвержены не притяжению Солнца, а воздействию опускающегося вниз (к Солнцу) внутреннего спирального потока. Наблюдающиеся отклонения в характере и направлении движения далеких спутников можно объяснить следующими причинами:
— участок орбиты большого диаметра далеких спутников располагается ближе к центру внутренней воронки опускающегося спирального потока, поэтому испытывают более сильное воздействие центростремительной силы от царящего там разрежения. Это приводит к вытягиванию орбиты в эллипс и повышению ее эксцентриситета;
— увеличение скорости опускающегося спирального потока по мере приближения к центру воронки, способствует более сильному давлению на поверхность спутника и смещению его орбиты вниз, что приводит к увеличению угла ее наклона к плоскости орбиты планеты;
— при достижении критического значения угла наклона и эксцентриситета орбиты (размещении ее участка вблизи воронки), спутник начинает вращаться под действием внутреннего спирального потока, т.е. в направлении противоположном вращению планеты.
Таким образом предложенная гипотеза позволяет объяснить особенности расположения и движения спутников относительно планет в Солнечной системе.
1. Емельянов Н. В. Практическая небесная механика. – М.: Физический факультет МГУ, 2018. 270 с.
2. Кузнецов А.И. Движение и вращение планет и звезд // Материалы Международной научно-практической конференции «ХI Торайгыровские чтения». – Павлодар, 2019. – Т. 4. – С. 3 – 8.
3. Мальцев Р.В., Ребров А.К. Газодинамические коллайдеры: численное моделирование. [Электронный ресурс]. – URL.: [Дата обращения 23.11.2020].
Космические скорости
«Поехали!»
В 1957 году работа советских учёных, конструкторов, инженеров, рабочих, во главе с Сергеем Павловичем Королёвым, увенчалась блестящей победой: 4 октября они вывели на орбиту первый в истории искусственный спутник Земли. А 12 апреля 1961 года отправили в первый космический полёт человека — Юрия Алексеевича Гагарина. На весь мир прозвучало знаменитое гагаринское «Поехали!», и человечество вступило в космическую эру.
Космическая тематика стремительно вошла в моду. Естественно, появились новые темы и понятия — ракеты, скафандры, невесомость, первая космическая скорость, вторая космическая скорость. Все мальчишки нашего поколения в мечтах примеряли скафандр космонавта. О невесомости мы поговорим в другой раз, а пока рассмотрим космические скорости.
Что известно о космических скоростях простым людям
На телевидении есть передача, в которой весёлый молодой человек бегает по улицам и задаёт прохожим разные вопросы. За правильный ответ он вручает 1000 рублей. Однажды он задал такой вопрос: «Какую скорость надо развить, чтобы оторваться от Земли?» Первый встречный ответить не смог, и ведущий буквально клещами вытащил из второго ответ, который был признан правильным: «Вторую космическую».
Увы, молодой человек ошибся. Вернее, ошибся не он, а редакторы, придумывающие вопросы и ответы к ним. Точно так, как и редакторы, считают почти все, кто хоть отдалённо слышал про существование первой и второй космических скоростей.
На самом деле, чтобы оторваться от Земли, подходит любая скорость. Уже когда ребёнок подпрыгивает, он отрывается от Земли. Пусть ненадолго, но отрывается. И вообще, до Луны или до другого космического объекта можно добраться с любой скоростью. Для этого надо немного разогнаться, а потом поддерживать силу тяги двигателя, равную силе земного притяжения, и вы будете «бороздить просторы Вселенной» с постоянной скоростью. Более того, если представить, что какой-то чудак сумел построить лестницу до Луны, то вы сможете подняться туда просто пешком. Примерно так, как вы поднимаетесь к себе домой на третий этаж, только гораздо дольше.
А как же космические скорости? Космические скорости подразумевают, что ракета, достигнув их, дальше летит к намеченной цели по инерции, с неработающим двигателем. Это только в мультфильмах про космические путешествия показывают летящие ракеты с работающим двигателем. Но это исключительно для создания иллюзии движения.
Если же в реальных условиях двигатель у ракеты будет работать постоянно, то даже для полёта на Луну потребуется такое количество топлива, что его ни одна ракета не осилит.
Постреляем
Первая космическая скорость
Первая космическая скорость — это скорость, с которой надо горизонтально запустить объект, чтобы он стал вращаться вокруг Земли по круговой орбите.
Чем больше высота, с которой мы запускаем объект, тем меньше эта скорость. Например, Международная космическая станция летает на высоте 400 км со скоростью 7,6 км/с, а Луна — на расстоянии 384 500 км от Земли со скоростью 1 км/с. «Нулевой» высоте соответствует скорость 7,9 км/с, что обычно и называют первой космической скоростью.
Точно так же Земля вращается вокруг Солнца почти по круговой орбите со скоростью ≈ 30 км/с. Это и есть первая космическая скорость относительно Солнца на таком расстоянии от него.
Если скорость спутника чуть больше первой космической для его высоты, его орбита будет эллипсом. Все спутники вокруг Земли и планеты вокруг Солнца движутся именно по эллипсам. И орбиты комет — тоже эллипсы, только очень вытянутые, так что кометы улетают по ним «в даль тёмную», лишь изредка возвращаясь к Солнцу «погреть бока».
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Вторая космическая скорость
Вторая космическая скорость — наименьшая скорость, которую необходимо придать космическому аппарату для преодоления притяжения планеты и покидания замкнутой орбиты вокруг неё.
Предполагается, что аппарат не вернётся на планету, улетит в бесконечность. На самом деле тело, имеющее около Земли такую скорость, покинет её окрестности и станет спутником Солнца. Вторая космическая скорость в \(\sqrt <2>≈ 1<,>4\) раза больше первой космической.
Третья космическая скорость
Третья космическая скорость — минимальная скорость, которую необходимо придать находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть притяжение не только Земли, но и Солнца, и покинуть пределы Солнечной системы.
Космические достижения
Первый искусственный спутник Земли был шариком диаметром 58 см и передавал только звуковой сигнал «бип-бип-бип». Но первая космическая скорость была достигнута! А всего через год, 2 января 1959 года, космический аппарат «Луна-1» полетел, естественно к Луне, со второй космической скоростью.
Пока с наибольшей скоростью 16,26 км/с покидала Землю автоматическая межпланетная станция «Новые горизонты», запущенная в США 19 января 2006 года. Относительно Солнца её скорость составляла 45 км/с — благодаря тому, что запускалась она в сторону движения Земли по орбите.
Конические сечения
Вернёмся к движению тела вокруг одного источника притяжения, например Солнца. Если тело запустить с первой космической перпендикулярно направлению на Солнце, оно полетит по окружности. Если запустить его в любом направлении, только не на само Солнце, со скоростью меньше второй космической, орбита будет эллипсом. При запуске со второй космической получится парабола. Если запустить с ещё большей скоростью, получится гипербола.
Эти кривые можно увидеть, пересекая конус плоскостью. Если ось конуса перпендикулярна плоскости, в пересечении получится окружность. Будем постепенно менять угол наклона плоскости к оси конуса. Линия пересечения превращается в эллипс, причём чем больше угол наклона, тем более вытянутым получается этот эллипс. Продолжим наклонять секущую плоскость до тех пор, пока она не станет параллельной одной из касательных плоскостей конуса. В этот момент линия пересечения — парабола. Наклоним ещё — получится гипербола.
Художник Мария Усеинова
1 Подробнее об этом читайте в «Квантике» №11 за 2016 год, с. 2–5.