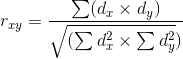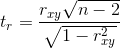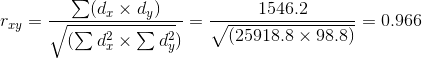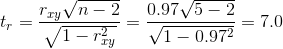Чем больше значение коэффициента корреляции тем
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
КРИТЕРИЙ КОРРЕЛЯЦИИ ПИРСОНА
– это метод параметрической статистики, позволяющий определить наличие или отсутствие линейной связи между двумя количественными показателями, а также оценить ее тесноту и статистическую значимость. Другими словами, критерий корреляции Пирсона позволяет определить, изменяется ли (возрастает или уменьшается) один показатель в ответ на изменения другого? В статистических расчетах и выводах коэффициент корреляции обычно обозначается как rxy или Rxy.
1. История разработки критерия корреляции
Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.
2. Для чего используется критерий корреляции Пирсона?
Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.
Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.
В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.
Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов.
4. Как рассчитать коэффициента корреляции Пирсона?
Расчет коэффициента корреляции Пирсона производится по следующей формуле:
5. Как интерпретировать значение коэффициента корреляции Пирсона?
Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Оценка статистической значимости коэффициента корреляции rxy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле:
Полученное значение tr сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает tкрит, то делается вывод о статистической значимости выявленной корреляционной связи.
6. Пример расчета коэффициента корреляции Пирсона
Целью исследования явилось выявление, определение тесноты и статистической значимости корреляционной связи между двумя количественными показателями: уровнем тестостерона в крови (X) и процентом мышечной массы в теле (Y). Исходные данные для выборки, состоящей из 5 исследуемых (n = 5), сведены в таблице:
Σ(X) = 951 + 874 + 957 + 1084 + 903 = 4769
Σ(Y) = 83 + 76 + 84 + 89 + 79 = 441
Mx = Σ(X) / n = 4769 / 5 = 953.8
My = Σ(Y) / n = 441 / 5 = 82.2
Корреляционный анализ
Корреляционный анализ
Корреляционный анализ – раздел математической статистики, исследующий зависимости между двумя или более случайными величинами. Термин «Correlation» означает взаимосвязь, взаимоотношение.
Функциональная зависимость и корреляция
Еще Гиппократ обратил внимание на то, что между телосложением и темпераментом людей, между строением их тела и предрасположенностью к заболеваниям существует определенная взаимосвязь.
В области физической культуры и спорта можно привести много примеров такой взаимосвязи. Например, от уровня силы во многом зависит результат, показанный спортсменом в таких видах спорта, как тяжелая атлетика, пауэрлифтинг, гиревой спорт, метание диска и толкание ядра и т.д. Результат в беге на 100 м во многом зависит от процента содержания в мышцах спортсменов быстрых мышечных волокон (II типа). Доказано, что у выдающихся спринтеров этот показатель превышает 80%. Чтобы определить, насколько сильна взаимосвязь между переменными (признаками) используется корреляционный анализ.
Две случайные величины X и Y могут быть:
В качестве меры связи между случайными величинами используется коэффициент корреляции. Коэффициент корреляции для генеральной совокупности обозначается ρ. Однако, как правило, он неизвестен. Поэтому он оценивается по экспериментальным данным, представляющим выборку объема n, полученную при совместном измерении двух переменных (признаков) X и Y. Коэффициент корреляции, определяемый по выборочным данным называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции). Его принято обозначать символом r. Наиболее часто в качестве оценок генерального коэффициента корреляции используется коэффициент корреляции Пирсона (r) и коэффициент корреляции Спирмена (rs).
Коэффициент корреляции Пирсона ( r )
Чтобы правильно применять корреляционный анализ в научных исследованиях, нужно учитывать условия применения этого метода.
Условия, при которых возможен расчет коэффициента корреляции Пирсона:
Коэффициент корреляции Спирмена ( r S)
При расчете коэффициента корреляции Спирмена требования к исходным данным менее строгие, а именно:
Свойства оценок коэффициентов корреляции
| n | 0,05 | 0,01 | 0,001 |
| 3 | 0,9969 | 0,999877 | 0,99999877 |
| 4 | 0,950 | 0,9900 | 0,9990 |
| 5 | 0,878 | 0,9597 | 0,99114 |
| 6 | 0,811 | 0,9172 | 0,9741 |
| 7 | 0,754 | 0,875 | 0,9509 |
| 8 | 0,707 | 0,834 | 0,9244 |
| 9 | 0,666 | 0,798 | 0,898 |
| 10 | 0,632 | 0,765 | 0,872 |
| 20 | 0,444 | 0,561 | 0,679 |
| 30 | 0,361 | 0,463 | 0,570 |
| 40 | 0,312 | 0,402 | 0,501 |
| 50 | 0,279 | 0,361 | 0,451 |
В итоговой таблице необходимо указать объем выборки, чтобы читающий мог оценить значимость (достоверность) вычисленных коэффициентов корреляции. Иногда в публикациях приводятся только значимые коэффициенты корреляции, а вместо незначимых ставится прочерк. В таблице 2 авторы указали, что объем выборки равен n = 32. Критическое значение коэффициента корреляции при n = 32 и a = 0,05 составляет r0,05 = 0,349 (В.С.Иванов, 1990). Следовательно, все коэффициенты корреляции достоверны.
Таблица 2 — Значения коэффициентов корреляции между результатами в скоростно-силовых тестах и результатом в толкании ядра с разгоном n=32, спортивный результат группы варьировал от 12,00 м до 20,50. Критическое значение коэффициента корреляции при n = 32 и a = 0,05 составляет r0,05 = 0,349 (по: Я.Е.Ланка, Ан.А.Шалманов, 1982).
Определение коэффициента корреляции
Опубликовано 20.05.2021 · Обновлено 20.05.2021
Что такое Определение коэффициента корреляции?
Статистику корреляции можно использовать в финансах и инвестировании. Например, коэффициент корреляции может быть рассчитан для определения уровня корреляции между ценой на сырую нефть и ценой акций нефтедобывающей компании, такой как Exxon Mobil Corporation. Поскольку нефтяные компании получают большую прибыль по мере роста цен на нефть, корреляция между двумя переменными очень положительная.
Понимание коэффициента корреляции
Есть несколько типов коэффициентов корреляции, но наиболее распространенным является корреляция Пирсона ( r ). Это измеряет силу и направление линейной зависимости между двумя переменными. Он не может фиксировать нелинейные отношения между двумя переменными и не может различать зависимые и независимые переменные.
Степень силы связи варьируется в зависимости от значения коэффициента корреляции. Например, значение 0,2 показывает, что между двумя переменными существует положительная корреляция, но она слабая и, вероятно, не важна. Аналитики в некоторых областях исследований не считают корреляции важными до тех пор, пока значение не превысит минимум 0,8. Однако коэффициент корреляции с абсолютным значением 0,9 или выше будет представлять очень сильную взаимосвязь.
Краткая справка
Инвесторы могут использовать изменения в статистике корреляции для выявления новых тенденций на финансовых рынках, в экономике и ценах на акции.
Ключевые моменты
Статистика корреляции и инвестирование
Другими словами, инвесторы могут использовать активы или ценные бумаги с отрицательной корреляцией для хеджирования своего портфеля и снижения рыночного риска из-за волатильности или резких колебаний цен. Многие инвесторы хеджируют ценовой риск портфеля, что эффективно снижает любой прирост капитала или убытки, потому что они хотят дивидендного дохода или доходности от акций или ценных бумаг.
Статистика корреляции также позволяет инвесторам определять, когда изменяется корреляция между двумя переменными. Например, акции банка обычно имеют очень положительную корреляцию с процентными ставками, поскольку ставки по кредитам часто рассчитываются на основе рыночных процентных ставок. Если цена акций банка падает, а процентные ставки растут, инвесторы могут понять, что что-то не так. Если цены на акции аналогичных банков в секторе также растут, инвесторы могут сделать вывод, что падение акций банков не связано с процентными ставками. Вместо этого плохо работающий банк, вероятно, имеет дело с внутренней фундаментальной проблемой.
Уравнение коэффициента корреляции
Чтобы вычислить корреляцию момента произведения Пирсона, необходимо сначала определить ковариацию двух рассматриваемых переменных. Затем необходимо вычислить стандартное отклонение каждой переменной. Коэффициент корреляции определяется делением ковариации на произведение стандартных отклонений двух переменных.
Стандартное отклонение – это мера разброса данных от среднего значения. Ковариация – это мера того, как две переменные изменяются вместе, но ее величина не ограничена, поэтому ее трудно интерпретировать. Разделив ковариацию на произведение двух стандартных отклонений, можно вычислить нормализованную версию статистики. Это коэффициент корреляции.
Часто задаваемые вопросы
Что подразумевается под коэффициентом корреляции?
Коэффициент корреляции описывает, как одна переменная движется по отношению к другой. Положительная корреляция указывает на то, что оба движутся в одном направлении с корреляцией +1,0, когда они движутся в тандеме. Отрицательный коэффициент корреляции говорит о том, что они движутся в противоположных направлениях. Корреляция, равная нулю, предполагает отсутствие корреляции вообще.
Как рассчитать коэффициент корреляции?
Коэффициент корреляции рассчитывается путем сначала определения ковариации переменных, а затем деления этой величины на произведение стандартных отклонений этих переменных.
Как используется коэффициент корреляции при инвестировании?
Коэффициенты корреляции – широко используемый статистический показатель в инвестировании. Они играют очень важную роль в таких областях, как состав портфеля, количественная торговля и оценка эффективности. Например, некоторые управляющие портфелями будут отслеживать коэффициенты корреляции отдельных активов в своем портфеле, чтобы гарантировать, что общая волатильность их портфелей поддерживается в допустимых пределах. Аналогичным образом аналитики иногда используют коэффициенты корреляции, чтобы предсказать, как на конкретный актив повлияет изменение внешнего фактора, такого как цена товара или процентная ставка.
Что означают положительный, отрицательный и нулевой коэффициенты корреляции?
Опубликовано 29.06.2021 · Обновлено 03.10.2021
Коэффициенты корреляции – это индикаторы силы линейной связи между двумя разными переменными x и y. Коэффициент линейной корреляции больше нуля указывает на положительную взаимосвязь. Значение меньше нуля означает отрицательную связь. Наконец, нулевое значение указывает на отсутствие связи между двумя переменными x и y. В этой статье объясняется значение коэффициента линейной корреляции для инвесторов, как рассчитать ковариацию для акций и как инвесторы могут использовать корреляцию для прогнозирования рынка.
Ключевые выводы:
Понимание корреляции
Коэффициент корреляции ( ρ ) – это мера, которая определяет степень, в которой связано движение двух разных переменных. Наиболее распространенный коэффициент корреляции, генерируемый корреляцией произведения-момента Пирсона, используется для измерения линейной связи между двумя переменными. Однако в нелинейной зависимости этот коэффициент корреляции не всегда может быть подходящей мерой зависимости.
Краткий обзор
При интерпретации корреляции важно помнить, что наличие корреляции между двумя переменными не означает, что одна вызывает другую.
Корреляция и финансовые рынки
На финансовых рынках коэффициент корреляции используется для измерения акции движутся в противоположных направлениях, коэффициент корреляции отрицательный.
Например, предположим, что цены на кофе и компьютеры наблюдаются и обнаруживают корреляцию +,0008. Это означает, что между двумя переменными нет корреляции или взаимосвязи.
Расчет ρ
Стандартное отклонение – это мера разброса данных от среднего значения. Ковариация – это мера того, как две переменные изменяются вместе. Однако его масштабы безграничны, поэтому его трудно интерпретировать. Нормализованная версия статистики вычисляется путем деления ковариации на произведение двух стандартных отклонений. Это коэффициент корреляции.
Положительное соотношение
Положительная корреляция – когда коэффициент корреляции больше 0 – означает, что обе переменные движутся в одном направлении. Когда ρ равно +1, это означает, что две сравниваемые переменные имеют идеальную положительную взаимосвязь; когда одна переменная движется выше или ниже, другая переменная движется в том же направлении с той же величиной.
Чем ближе значение ρ к +1, тем сильнее линейная зависимость. Например, предположим, что стоимость цен на нефть напрямую связана с ценами на авиабилеты с коэффициентом корреляции +0,95. Взаимосвязь между ценами на нефть и стоимостью авиабилетов имеет очень сильную положительную корреляцию, так как значение близко к +1. Таким образом, если цена на нефть снижается, цены на авиабилеты также уменьшаются, а если цена на нефть растет, то же самое происходит и с ценами на авиабилеты.
На приведенной ниже диаграмме мы сравниваем один из крупнейших банков США, JPMorgan Chase & Co. ( биржевым фондом Financial Select SPDR Exchange Traded Fund (ETF) (XLF ).1 Как вы понимаете, компания JPMorgan Chase & Co. должна иметь положительную корреляцию с банковской отраслью в целом. Мы видим, что коэффициент корреляции в настоящее время составляет 0,98, что свидетельствует о сильной положительной корреляции. Значение выше 0,50 обычно свидетельствует о положительной корреляции.
Понимание корреляции между двумя акциями (или одной акцией) и отраслью может помочь инвесторам оценить, как акции торгуются по сравнению с аналогами. Все типы ценных бумаг, включая облигации, сектора и ETF, можно сравнить с помощью коэффициента корреляции.
Отрицательная корреляция
Примеры отрицательной корреляции
Когда дело доходит до инвестирования, отрицательная корреляция не обязательно означает, что следует избегать ценных бумаг. Коэффициент корреляции может помочь инвесторам диверсифицировать свой портфель, включив в него набор инвестиций, имеющих отрицательную или низкую корреляцию с фондовым рынком. Короче говоря, при снижении риска волатильности в портфеле иногда все же привлекаются противоположности.
Коэффициент линейной корреляции
Даже для небольших наборов данных вычисления коэффициента линейной корреляции могут оказаться слишком длинными, чтобы их можно было выполнять вручную. Таким образом, данные часто загружаются в калькулятор или, что более вероятно, в компьютер или статистическую программу, чтобы найти коэффициент.
Коэффициент Пирсона
Простая линейная регрессия описывает линейную связь между переменной ответа (обозначенной y) и независимой переменной (обозначенной x) с использованием статистической модели. Статистические модели используются для прогнозов.
Краткий обзор
Упростите линейную регрессию, вычислив корреляцию с помощью такого программного обеспечения, как Excel.
В финансах, например, корреляция используется в нескольких анализах, включая расчет стандартного отклонения портфеля. Поскольку это требует много времени, корреляцию лучше всего рассчитать с помощью такого программного обеспечения, как Excel. Корреляция объединяет статистические концепции, а именно дисперсию и стандартное отклонение. Дисперсия – это дисперсия переменной вокруг среднего значения, а стандартное отклонение – это квадратный корень из дисперсии.
Поиск корреляции с помощью Excel
В Excel есть несколько методов расчета корреляции. Самый простой – получить два набора данных рядом и использовать встроенную формулу корреляции:
Если вы хотите создать корреляционную матрицу для ряда наборов данных, в Excel есть подключаемый модуль анализа данных, который находится на вкладке «Данные» в разделе «Анализ».
Выберите таблицу доходов. В этом случае наши столбцы имеют заголовки, поэтому мы хотим установить флажок «Ярлыки в первой строке», чтобы Excel обрабатывал их как заголовки. Затем вы можете выбрать вывод на том же листе или на новом листе.
Как только вы нажмете Enter, данные будут созданы автоматически. Вы можете добавить текст и условное форматирование, чтобы очистить результат.
Часто задаваемые вопросы о коэффициенте линейной корреляции
Что такое коэффициент линейной корреляции?
Коэффициент линейной корреляции – это число, вычисленное на основе заданных данных, которое измеряет силу линейной связи между двумя переменными, x и y.
Как найти коэффициент линейной корреляции?
Корреляция объединяет несколько важных и связанных статистических концепций, а именно дисперсию и стандартное отклонение. Дисперсия – это дисперсия переменной вокруг среднего значения, а стандартное отклонение – это квадратный корень из дисперсии.
Вычисления слишком длинные, чтобы их можно было выполнять вручную, и программное обеспечение, такое как Excel или статистическая программа, является инструментами, используемыми для вычисления коэффициента.
Что подразумевается под линейной корреляцией?
Как найти коэффициент линейной корреляции на калькуляторе?
Графический калькулятор необходим для расчета коэффициента корреляции.Следующие инструкции предоставлены Statology.
Шаг 1. Включите диагностику
Вам нужно будет сделать этот шаг на калькуляторе только один раз. После этого вы всегда можете начать с шага 2 ниже. Если вы этого не сделаете, r (коэффициент корреляции) не будет отображаться при запуске функции линейной регрессии.
Нажмите [2nd], а затем [0], чтобы войти в каталог вашего калькулятора. Прокрутите, пока не увидите «DiagnosticsOn».
Нажимайте Enter, пока на экране калькулятора не появится надпись «Готово».
Это важно повторить: вам никогда не придется делать это снова, если вы не перезагрузите калькулятор.
Шаг 2: введите данные
Введите свои данные в калькулятор, нажав [STAT], а затем выбрав 1: Edit. Чтобы упростить задачу, вы должны ввести все свои «данные x» в L1 и все «данные y» в L2.
После того, как вы введете свои данные, вы перейдете к [STAT], а затем к меню CALC вверху. Наконец, выберите 4: LinReg и нажмите Enter.
Это оно! Готово! Теперь вы можете просто считать коэффициент корреляции прямо с экрана (его r). Помните, что если r не отображается на вашем калькуляторе, необходимо включить диагностику. Это то же самое место на калькуляторе, где вы найдете уравнение линейной регрессии и коэффициент детерминации.
Коэффициент линейной корреляции может быть полезен при определении взаимосвязи между инвестициями и рынком в целом или другими ценными бумагами. Его часто используют для прогнозирования доходности фондового рынка. Это статистическое измерение полезно во многих отношениях, особенно в финансовой отрасли. Например, это может быть полезно для определения того, насколько хорошо взаимный фонд ведет себя по сравнению с его эталонным индексом, или его можно использовать для определения того, как взаимный фонд ведет себя по отношению к другому фонду или классу активов. Добавляя взаимный фонд с низкой или отрицательной корреляцией к существующему портфелю, можно получить преимущества диверсификации.